Overview

This is just random variables which account for non-discrete values.

Definitions

f_{X} (x) = \frac{1}{2 π σ^{2}} e^{- (x - μ)^{2} / 2 σ^{2}}

Where $μ$ can be any real number and $σ > 0$

It has expected value and variation

E [X] = μ V a r [X] = σ^{2}

It's CDF is

F_{X} (x) = Φ (\frac{x - u}{σ})

The probability that $X$ is in the interval $(a, b]$ is

P [a < X \leq b] = Φ (\frac{b - μ}{σ}) - Φ (\frac{a - μ}{σ})

Φ (z) = \frac{1}{2 π} \int_{- \infty}^{z} e^{- u^{2} / 2} d u

Note

There is also a table that is much more commonly used.

The $z$ value can be understood as

z = \frac{x - μ}{σ}

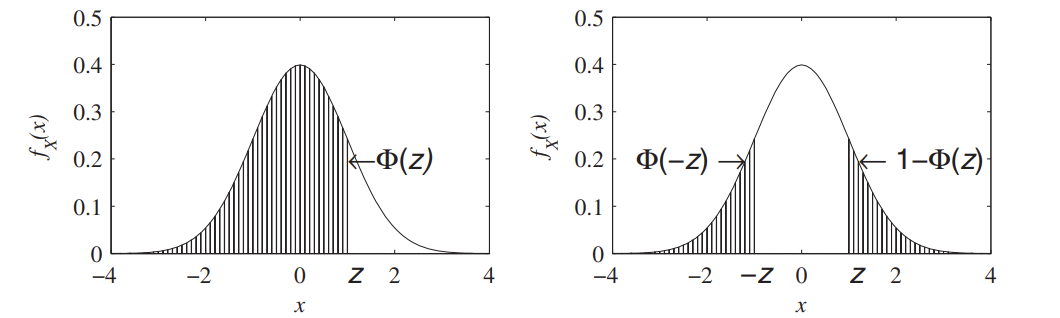
Pasted image 20241029094716.png

Can be understood as

Q (z) = P [Z > z] = \frac{1}{\sqrt{2 π}} \int_{z}^{\infty} e^{- u^{2} / 2} d u = 1 - Φ (z) .

Φ (- z) = 1 - Φ (z)