Overview

As the name suggest this focuses on Linear Equations explicitly.

A Linear Equation is one that contains variables manipulated by reversable operations. Variables can be manipulated by constants which are multiplied, divided, added, and subtracted.

Systems of Linear Equations

There are 3 operations that can be performed on Linear Systems:

Interchanging two equations
Multiply one equations by a nonzero number
Add the multiple of one equation to another

All linear equations will fall under one of these three types of solutions:

No solution
One unique solution
$\infty$ solutions

NOTE: This will not occur for non-linear equations

Solving Systems of Linear Equations

Linear equations should only be simplified using invertible processes. This can be one of the three following operations:

Changing the order of equations.
Multiply an equation by an a non-zero constant.
Add or subtract a multiple of an equation to another.

Augmented Matrix Notation

Elementary Operations

Interchange two rows
Multiply one row by a scalar
Add a multiple of one row to another

$\forall$ Examples

Interchange Two Rows

$R_{i} \leftrightarrow R_{j}$

Multiply a Row by a Scalar $C$

$R_{i} \to C \cdot R_{i}$

e.g. $R_{1} \to R_{1}$

Add a multiple of a Row to Another

$R_{i} \to C \cdot R_{j} + R_{i}$

Definitions:

Augmented Matrices:

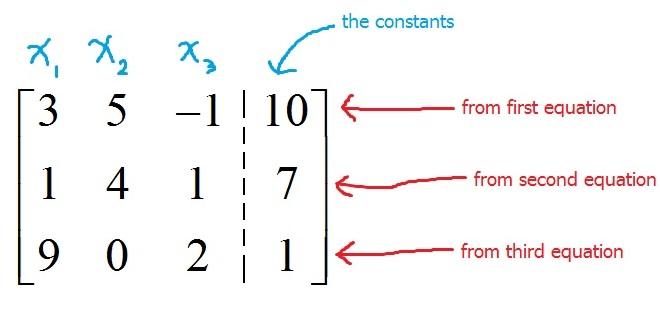
Pasted image 20230823113640.png

Gaussian Elimination:
#gaussian-elim

Put 1 in the top left col.
Use this leading 1 to eliminate all other value in that column
Repeat this process for each remaining row.

Row Echelon Form (REF) :
#echelon-form

A matrix is in echelon form if:

All zero rows are at the bottom.
The left most non-zero entry (leading 1 or pivot point ), of each row is to the right of the leading 1 from the row above.

Reduced Row Echelon Form (RREF):

A matrix is reduced if:

It is in echelon form. #echelon-form
A leading $1$ is the only non-zero value in the column.

Using row elimination operations, any system can be simplified in RREF. Moreover this reduced form is unique.

This process is also called gaussian elimination #gaussian-elim

Theorem: If A is Invertible then RREF of A is I

Leading Variable:

A leading variable is one that is defined by other variables and constants. If represented in REF this would be the variable represented by a column with a leading 1 (pivot point).

Free Variable:

A free variable one is that is defined by other variables and constants. If represented in REF this would be the variable represented by a column with a leading 1 (pivot point).

Homogeneous Systems

A homogeneous (linear) system is one in which every RHS is 0

e.g.

| \begin{matrix} 1 & 2 & 0 \\ 2 & 2 & 0 \\ 0 & 6 & 0 \end{matrix} |

Note: Homogeneous system have many nice (special) properties!

Basic Properties of Homogeneous Systems:

There is always one trivial solution; i.e. set all unknown vars = 0
There is a Dichotomy of solutions, the trivial solution or $\infty$ many
A Linear Combo of solutions to a homogeneous system is also a solution. #linear-combo

Applications

Ancient Greeks

Any two distinct points determine a line.

Any 3 points that do not lie on the same line determine a circle.

Any 5 points provided that any 4 are not co-linear determine a conic.