Definition:

The basic idea behind the an integral is to find the area under a curve of a function. This extends the idea of a Reimann Sum by creating infinitely small "rectangles" that we add up in order to get the area of a curve.

Indefinite Integrals:

An indefinite integral is essentially the inverse operation to taking a derivative, this may also known as an anti-derivative.

Improper Integrals:

Type 1: Infinite Bounds

This occurs when one of the bounds of an integral from $a$ to $b$ are equal to $\infty$ .

This can be dealt with by reorganizing the integral's bounds. We will instead take the limit as a variable R goes to infinity and replace the infinity in the bound with R such that:

\int_{a}^{\infty} f (x) d x = lim_{R \to \infty} \int_{a}^{R} f (x) d x

From there the integral can be solved as a proper integral keeping in mind the bound is a limit.

Theorem 1: the p-integral over $[a, \infty)$

Type 2: Infinite Discontinuity

This is when there is an infinite break (usually a vertical asymptote sometimes another asymptote) in-between the bounds of the function to be integrated.

This is dealt with by breaking the integral into two different parts and taking the limit where the function approaches the asymptote such that:

\int_{- 2}^{2} \frac{1}{x} = lim_{R \to 0} \int_{- 2}^{R} + \int_{R}^{2}

Area Between Curves

There are two different types of areas, Vertically Simple and Horizontally Simple.

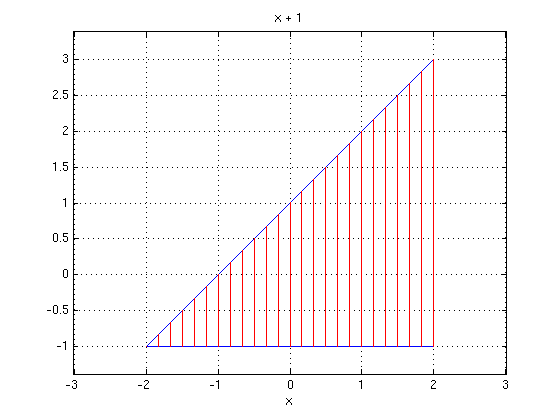
Vertically Simple

If a vertical line is drawn and pushed through the area between two curves from $a$ to $b$ and:

The line touches both functions at exactly one point each.
One function's $y$ values are always greater than the other's on the interval ( $a$ , $b$ )

the area is vertically simple.

ex.

$vertically simple$

Horizontally Simple

If a horizontal line is drawn and pushed through the area between two curves from a to b and:

The line touches both functions at exactly one point each.
One function's $x$ values are always greater than the other's on the interval (a,b)

the area is horizontally simple.

ex.

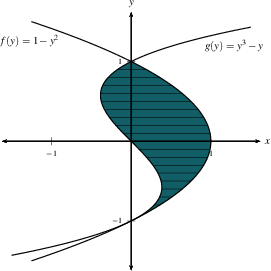
horizontally simple

Finding the Area Between Curves

The area of a curve can be found by taking the integral of the outer function minus the inner function along the vertically or horizontally simple region's interval.

e.g. Given $y = \sqrt{x}$ and $y = \frac{x}{2}$ :

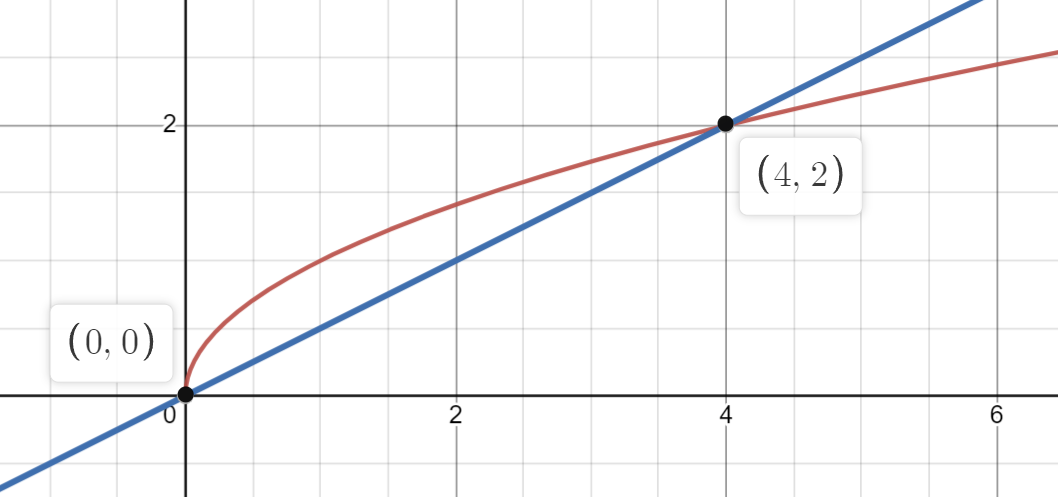
Pasted image 20230411152411.png

The area under the curve is: $$\int_{0}^{4}x^{2}-\frac{x}{2}dx$$

Advanced Integration Techniques

U-Substitution

This is mostly useful when solving simpler two product integrals in the form $\int u (x) v (x) d x$ where $u (x)$ or a subsequent "part" can be substituted by the derivative of $v (x)$ or vice versa.

e.g. Given $\int \cos (x) \sin^{2} (x) d x$ we could choose $u = \sin (x)$ which would make $d u = \cos (x) d x$ .

Substituting in $u$ and $d u$ we come back with the equation:

\int u^{2} d u

Which is a fairly simple integral to solve using the power rule:

\begin{aligned} \int u^{2} d u & = \frac{u^{3}}{3} + C \\ = \frac{\sin^{3} (x)}{3} + C \end{aligned}