Overview

Graphs represent a set of objects (vertices) where some objects are connected (edges). Graphs have many uses in computer science.

There are two basic types of graphs. directed and undirected graphs.

Types

Directed Graphs

Also known as digraphs, these are graphs where edges are one-directional. This means that an edge pointing from $(a \to b)$ is not the same as and edge pointing from $(b \to a)$ . These graphs can also contain self-loops, or an edge that points from a vertex back to itself $(a \to a)$ .

Undirected Graphs

These are graphs where edges are bi-directional. This means an edge from ( $a \to b$ ) is the same as and edge from ( $b \to a$ ). These graphs cannot contain self-loops.

Weighted Graphs

Weighted graphs can be both directed or undirected. They simply assign a value to each edge of the graph. This can be used to find optimal paths through a graph.

DAG

A Directed acrylic graph (DAG) is a directed graph with no cycles.

DAG's can be topologically sorted.

Topological Sort

A topological sort is a linear ordering of all the vertices in a DAG such that if it contains an edge $(u, v)$ then $u$ appears before $v$ in the ordering.

It is useful for sequencing tasks with dependency constraints.

Note

This is not a comparison based sort and specifically applies to DAGs. When a graph contains a cycle no linear ordering is possible.

Using DFS can perform topological sort in $Θ (V + E)$ time.

Trees

Free Tree

A free tree is a graph with the following conditions met:

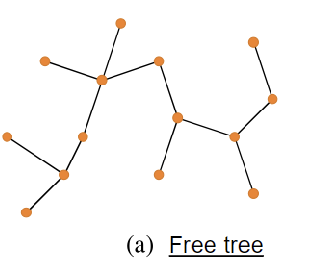
Pasted image 20240505095754.png

Note

A free tree with a designated root node is called a rooted tree.

The following properties are found in free trees:

Any two vertices are connected by a unique simple path
The number of edges is one less than the number of vertices
If any existing edge is removed, the resulting graph will be disconnected.
If any new edge is added between two vertices, the graph will contain a cycle

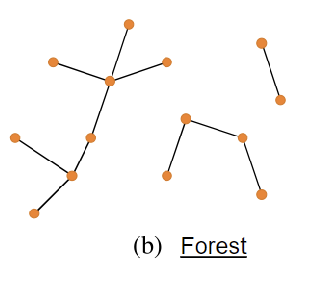
Forests

A forest meets most of the same conditions as a free tree, except that it is disconnected (i.e. the number of #Connected Components > 1).

Undirected
Disconnected (connected components > 1)
Acyclic (not cyclic)

Pasted image 20240505095805.png

Spanning Tree

For a connected undirected graph, its spanning tree is a free tree that contains:

All the vertices in the graph
Edges in the tree are a subset of all the edges in the graph

i.e. Let a graph $G = (V, E)$ and tree $T = (V, A)$ then:

\begin{array}{r} G (V) = T (V) \\ T (A) \subset G (E) \end{array}

Minimum Spanning Tree

A minimum spanning tree (MST) can only exist on a weighted graph and is a spanning tree with the least total cost (weight) in the set of its edges.

Note

The MST of a weighted graph may not be uniuque.

Representations

There are two standard ways to represent graphs which apply for both #Directed Graphs and #Undirected Graphs. Each method has its own upsides and downsides.

Collection of Adjacency lists
- Good way to represent a #Sparse Graph.
- Common method of choice
Adjacency matrix
- Good way to represent a #Dense Graph.
- Also good for quickly checking if an edge connects two given vertices.
- Used when there are a large number of vertices and edges.

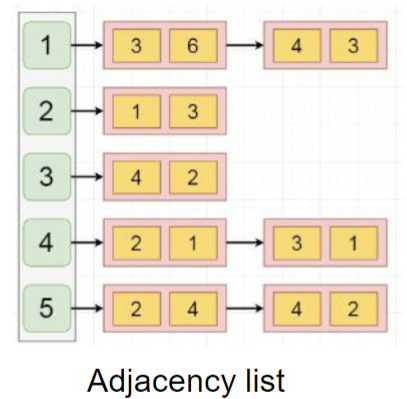
Adjacency List

This consists of a collection of lists where each index, key, etc. corresponds with a linked-list which contain each adjacent vertex node.

A collection can be a hash map, array, or even another linked-list.

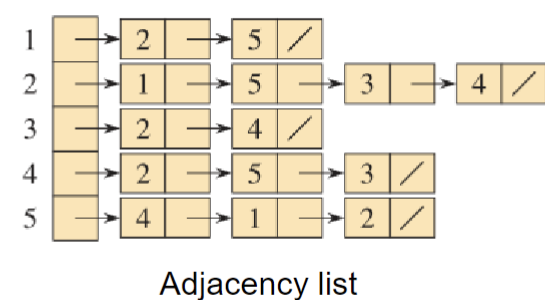
Pasted image 20240502150331.png

For weighted graphs we can just add the weight next to the adjacent vertex in each list.

Pasted image 20240502152829.png

Adjacency matrix

This consists of an $n \times n$ matrix where n is the number of vertices in the graph such that each index in a row/column corresponds with a vertex in the graph. If an edge exists then the item at the corresponding entry is marked with a 1. The matrix is always symmetric across the diagonal if the graph is directed.

i.e where A is the matrix, and E represents the edges in a graph.

A_{i j} = {\begin{cases} 1 & (i, j) \in E \\ 0 & otherwise \end{cases}

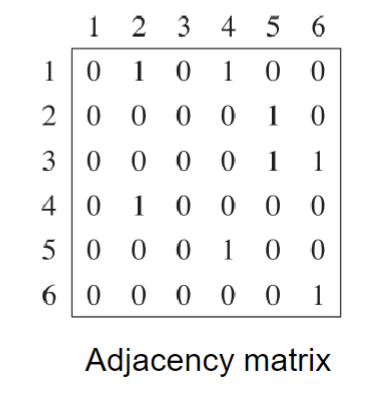
Pasted image 20240502152853.png

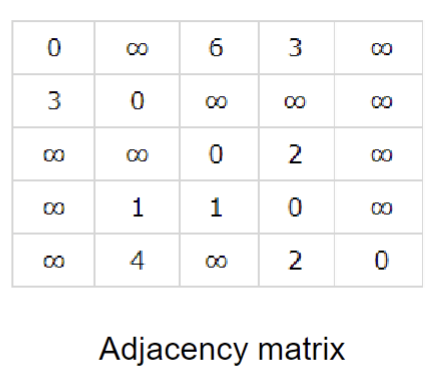
For weighted graphs we just relace the value at the entry representing each edge with the corresponding weight. All other values are infinite.

Pasted image 20240502153314.png

Definitions

Adjacency

Adjacency is defined as any vertex (b) connected to a given vertex (a).

For directed graphs adjacency is not necessarily symmetric. This means if an edge from ( $a \to b$ ) exists we can say that a is adjacent to b. However if the edge from ( $b \to a$ ) does not exist we cannot say that b is adjacent to a.

For undirected graphs adjacency is symmetric. This means if an edge exists from ( $a \to b$ ) then a is adjacent to b and vice versa.

Degree

The degree of a vertex is the number of edges connecting it to or from other vertices in a graph.

For directed graphs there are three different classifications of degrees, in-degree, out-degree and total-degree.

The in-degree is defined as the number of edges that point to the vertex. The out-degree is defined as the number of edges that point out of the vertex. The total-degree is the sum of the in-degree and out-degree

For undirected graphs the degree is just the number of edges that connect the given vertex to another vertex.

Sparse Graph

A graph in which the number of edges are considerably smaller than the maximum number of potential edges.

i.e. $E < V^{2}$ where E is the number of edges and V is the number of vertices.

Dense Graph

A graph in which the number of edges are very close to the maximum number of potential edges.

i.e. $E \approx V^{2}$ where E is the number of edges and V is the number of vertices.

Path

A path in a directed graph is a sequence of vertices, $⟨ v_{1}, v_{2}, . . . v_{k} ⟩$ such that there is an edge connecting each consecutive pair of vertices

Cycle

A cycle is a path $⟨ v_{1}, v_{2}, . . . v_{k} ⟩$ in a directed graph where $v_{1} = v_{k}$ . i.e. the first and last vertices in the sequence are the same.

Connected Components

In an undirected graph a connected component is a subset of all the vertices in a graph where all the vertices in the graph are connected by a #Path.

If a graph only has one connected component it is said to be a connected graph.

Finding connected components is useful for identifying clusters of connections in a graph.

Implementations

The first method is to use a graph searching algorithm like DFS or BFS. This will find all the connected components for a given vertex, but to find all connected component we have to search through all the vertices.

The second method is to use a disjoint set. This makes a new set for each vertex and unions all the adjacent vertices for each vertex. This will create the final connected components for the entire graph.

Path Weight

This is the sum of the weight of all the edges in a path.

Reference

Sun, Hongyang Various lectures The University of Kansas 2024

Data Structures

Overview

Types

Directed Graphs

Undirected Graphs

Weighted Graphs

DAG

Topological Sort

Trees

Free Tree

Forests

Spanning Tree

Minimum Spanning Tree

Representations

Adjacency List

Adjacency matrix

Definitions

Adjacency

Degree

Sparse Graph

Dense Graph

Path

Cycle

Connected Components

Implementations

Path Weight

Reference

Related