Overview

There are multiple different cipher algorithms we can utilize to obscure data.

Cipher Design

Cipher design can make use of the following techniques.

Substitution

One set of bits is exchanged for another.

Example

  • One letter is replaced by another
  • One (block of) byte(s) is replaced by another (block of) byte(s)

The issue with substitution is there same order of keys is used. Which makes it vulnerable to frequency analysis.

Transposition

Rearrange the order of ciphertext to break the repeated patterns in the plaintext.

Example

Rearrange based on its location in the plaintext through permutation.

Confusion

Make the relationship between the plaintext and ciphertext (or ciphertext and key) as complicated as possible.

This uses the key in a very complex such that changes in the plaintext affect the ciphertext in an unpredictable way.

Diffusion

Dissipate the statistical structure of the plaintext in the long range statistics of the ciphertext.

The goal here is to have plaintext characters (bits) affect each ciphertext character (bit). This aims to have any change in the plaintext affect many parts of the ciphertext.

Shannon Secrecy

Claude Shannon, who came up with Shannon secrecy is also known as the "Father of Information Theory".

Shannon secrecy states the following:

P[M=m|c=E(K,m)]=P[M=m]
Abstract

The probability of guessing the plaintext given the ciphertext is known as a function of E, P[M=m|c=E(K,M)], is the same as the probability of guessing the ciphertext, P[M=m].

P[c=E(K,m)]=P[c=E(K,m′)]
Abstract

The probability of any message giving a ciphertext is the same.

Shannon's Theory: A Cipher achieves perfect secrecy if and only if there are as many possible keys as possible plaintexts, and every key is equally likely.

Shannon introduced the idea of #Substitution-Permutation Networks.

Substitution-Permutation Networks

Also known as S-P networks, this based on a combination of substitution and permutation. Substitution is done using an S-box and permutation is done using a P-box. They provide confusion and diffusion respectively.

Kerckhoff's Principle

Quote

The system must not be required to be a secret, and it must be able to fall into the hands of the enemy without inconvenience.

Trying to conceal your algorithm is infeasible, so instead security must rely on the secrecy of the key. The key should have randomness and it should be kept secret.

One-Time Pad

One-Time Pad or OTP is an encryption technique that cannot be cracked (in theory). It requires the use of a single use pre-shared key that is larger than or equal to the size of the plaintext to be encrypted. Each bit or character of the plaintext is encrypted by combining it with the corresponding bit or character of the pad using modular addition.

Note

Modular addition can be achieved in binary with the XOR operation.

This is because of the following:

  1. k⊕k=0
  2. p⊕0=p
  3. p⊕k⊕k=p

This makes OTP very easy to compute.

The following must be true for OTP to be impossible to decrypt or break:

  1. The key must be at least as long as the plaintext
  2. The key must be truly random
  3. The key must never be reused in whole or part
  4. The key must be kept completely secret by the communicating parties

In reality it is not possible for all of these conditions to be met.

In addition there are a few other issues with OTP:

Classic Ciphers

Substitution Cipher

A substitution cipher takes a character (or sequence of bytes) and substitute it for another character (or sequence of bytes).

A key maps a set of characters (or bytes) to the same set off characters (or bytes) but transformed in some way.

Note

A monoalphabetic cipher is a type of substitution cipher that works for letters of an alphabet.

Caesar Cipher

This is a very simple cipher which takes an ordered alphabet and shifts the characters in the alphabet by some natural number value.

Note

This is a shift cipher which is a sub-type of substitution cipher.

Given a key of K, encryption works by taking each character in some plaintext and shifting it K characters, then mod-ing it with the length of the set of all possible characters.

Decryption works similarly, except the given character is subtracted by the key K and then mod-ed by the length of the alphabet

Example

Given an ordered alphabet of [a...z] and |[a...z]|=26 we can define encryption and decryption as the following

EncryptionEK(c)=(c+K)%26DecryptionDK(c)=(c−K)%26

Breaking the this cipher is extremely easy as there are a limited number of shifts (26 - 1 = 25 given an alphabet of only lowercase English letters) we can try before we get some readable plaintext back.

Vigenère Cipher

The vigenere cipher constructs a table, often called a vigenere table, where each row in the table is a different shift of the alphabet. A key is the sequence of rows used to encrypt the *plaintext.

Example

We can use the key "SECRET" to shift each character in some message by the row that maps to S, E, C, R, E and T and just repeat the key when the length of the message is greater than the length of the key.

This is cipher is much more robust against Cryptanalysis#Frequency Analysis as it can map one character to multiple different shifts. It also requires more guesses, and therefore more computation, to find possible plaintexts.

Note

It is not required to generate the entire table to calculate the ciphertext. We can just use the formula for a #Caesar Cipher and replace each K with the corresponding key value

Symmetric Encryption

Symmetric encryption uses a single key for both encryption and decryption. It is a simple and strong form of encryption (most of the time).

Data Encryption Standard

The Data Encryption Standard cipher or DES was first proposed by IBM in 1975 and standardized by NBS (NIST) in 1976.

Note

This was the federal standard for 26 years before AES replaced it in 2002. It is not and should not be used anymore due to its many vulnerabilities.

DES is a block cipher with a block size of 64 bits and a key length of 56 bits there are an additional 8 bits for parity. Each block is a Feistel structure, which is a mathematical symmetric structure.

Diagram of Structure

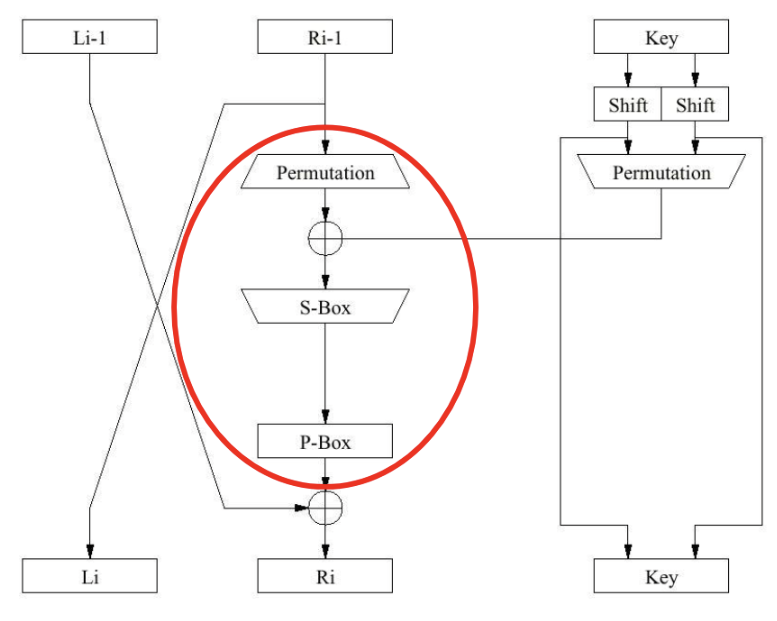
Pasted image 20241017094000.png

Warning

Putting the plaintext through this structure only once can leaves us with a major security flaw. The left-half of the block is "un-mangled" and just placed on the right-half of the resulting ciphertext. To avoid this multiple iterations of this mangling are done, these are called rounds. DES contains 16 rounds.

Decryption is done the same way, except the round keys are used in the reverse order.

Advanced Encryption Standard

Definitions

Monoalphabetic Substitution Cipher

This employs one ordered alphabet to generate the ciphertext, an example would be the #Caesar Cipher.

**Polyalphabetic Substitution Cipher

This employs many ordered alphabet to generate the ciphertext, an example would be the #Vigenère Cipher.

Block Cipher

A block cipher works over chunks ("blocks") of plaintext.

For a block of N bits, we have a total of 2N! permutations.

Feistel Structure

This is a symmetric structure in which operations are reversible. This means we can use the same operation in both encryption and decryption.

Warning

This is inherently insecure, since one half is not encrypted we already have half the input. The solution to this is using rounds.

Rounds

Rounds involves using the same basic operation multiple times. Its purpose is to make encryption harder to crack and keep the original information.

Key Length

Length of the key used in encryption.

Key Space

All possible keys that can be generated.

Reference

  1. Li, Fengjun Various, Lectures University of Kansas 2024

Related