Overview

Finding MSTs stems from a #Generic Method that grows the tree by adding one edge at a time.

Generic Method

The generic method starts with an empty tree and grows the MST by adding one #Safe Edge at a time.

def generic_mst(graph):
	tree = []
	while tree != spanning_tree:
		edge = graph.safe_edge
		tree.push(edge)
	return tree

Kruskals

This method keeps uses a disjoint set to keep track of a forest of possible MSTs.

• Start with a forest of singleton vertices.
• The edges are processed in increasing order of weight.
• At each iteration, find an edge that connects two trees and has the lowest weight and add it to the final MST. This is guaranteed to be safe.
• The process repeats until all trees are connected.

def mst_kruskals(graph):
	mst = {}
	forest = DisjointSet()
	for vertex in graph.vertices:
		forest.makeSet(vertex)
    # Make sure to sort by weight and increasing order
	graph.edges.sort()
	for (u, v) in graph.edges:
		# Check if the edges belong to the same set
		if forest.parent(u) != forest.parent(v):
			mst.add((u, v))
			forest.union(u, v)
	return mst

Prims

Running Time: $O(E\log V)$

Link to min-heap when doc is created.

This method always maintains a single tree instead of a forest. A min-priority queue is used to keep track of all vertices not added to the final MST.

• The tree starts from an arbitrary root vertex.
• At each iteration, it adds the minimum-weight edge adjacent to the current vertex to the final MST. This is guaranteed to the safe.
• The process repeats until all vertices are added to the tree.

mst_prim(graph, root):
	# Initalize the vertices
	for vertex in graph.vertices:
		vertex.key = float('inf')
		vertex.predecessor = None
	# Initalize the root vertex and start the queue
	root.key = 0
	min_queue = MinHeap()
	# Add all the vertices to the queue
	for vertex in graph.vertices:
		min_queue.add(vertex)
	# While the queue is not empty
	while not min_queue.is_empty:
		# Add to the MST
		u = min_queue.dequeue()
		# Update the keys of adjacent vertices
		for v in graph.adj[u]:
			if v in min_queue and graph.weight(u, v) < v.key:
				v.predecessor = u
				v.key = graph.weight(u, v)
				min_queue.heapify()

The final MST is given by: $A=\{(v,v.\pi ):v\in V-\{r\}\}$

MST = [(u, v) \
	   for u in graph.vertices \
	   for v in graph.adj[u] \
	   if v.predecessor != v and v == u.predecessor]

Definitions

Cut

A cut is defined as the partitioning of all the vertices in a graph into two disjoint subsets by set grouping.

i.e. let a graph $G=(V,E)$, a cut would be $(S,V-S)$ separating the vertices in the graph into two disjoint subsets $S$ and $V-S$.

e.g. the orange and tan vertices form a cut (the red line).

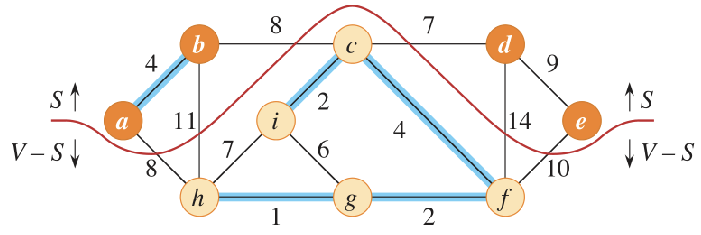
Cross

An edge crosses the cut if one end of the edge belongs to one disjoint set and the other edge belongs to the other.

i.e. an edge $(u,v)\in E$ crosses if $u\in S$ and $v\in S-V$ or vice versa.

e.g. $(a,h)$ crosses the cut; $(h,i)$ does not.

Respect

A cut respects a set A (tree to be built) if no edge in A crosses the cut.

e.g. the cut respects the set of blue edges

Safe Edge

An edge is considered "safe" if the following conditions are met.

• There exists a cut that respectes s A (the MST found so far)
• There is an edge that crosses the cut and its weight is the minimum among all edges crossing the cut

Reference

1. Sun, Hongyang MST The University of Kansas 2024

Related

• Algorithms
• Graphs